"C-stack" Experiments

“C-stack” Experiment

Casey Rodgers

8/21/2012

            Looking at alternative energy concepts on a website [1] I found an article written by Cris Paltenghe. He claimed that the device disobeyed a well known energy law that works for capacitors in an alternating circuit which is simply:

 (formula 1)

 Where W = energy, C = capacitance, and V = voltage. 

It is a very simple experiment to duplicate and since I had the materials I replicated it with a frequency generator, an oscilloscope, and some copper sheet capacitors which have silicon as the dielectric. I put two of these together with wax paper. I haven’t bonded them together with glue or anything but when I used a capacitor tester my dad owns the range of capacitance is around plus or minus 100pF. The test setup is shown in the pictures below:

This is the frequency generator I used.

 This is the oscilloscope I used which hooks up to my computer.

This is the C-stack with leads taped to it.

 

             I ran a few initial tests by tuning the device to a resonant frequency where the output would have the highest voltage. I found that there definitely is an anomaly with the energy stored and discharged in the capacitor over AC cycle using the simple formula 1. With no way of testing the current in the device I decided to try and calculate the power across the device using conventional AC circuitry formulas (e.g. reactance, impendance, and RC series formulas) [2,3].

After running these tests I realized that maybe there is a correlation between the equations for transformers and the “c-stack” which is essentially a capacitive transformer. Using the simple equation for voltage in a capacitor and then making a ratio of these terms. Looking at this formula I came up with the hypothesis that if the circuit were modified with an increase in capacitance on either the input or the output, the voltage would change. To do this a third capacitor was placed in parallel across the c-stack on the input and then the output and none at all for control.  For each test the frequency was adjusted to find a resonant spot that would have a peak in the secondary voltage.

           Starting with the simple equation for voltage in a capacitor I made a ratio of these for the “primary” (or outer capacitor side) to the “secondary” side.

This formula then makes a ratio equation:

Then re-arranged forms an equation that I used to make two predictions for an experiment.

 

These predictions are: 1) If the input capacitance (C_1) were increased, the output voltage (V_2) should increase. 2) If the output capacitance (C_2) were increased the output voltage (V_2) should decrease.

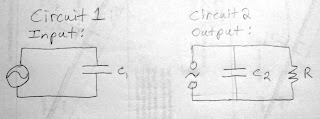
            The circuit setup was a frequency generator attached to the C-stack and the output of which had a resistor (see figure 1). To do the AC circuit analysis I treated the input as one circuit and the output as another (see figure 2). The third capacitor is not shown in the figures but was placed on the input, then the output and not at all for the control test.

                                                                       Figure 1

 

                                                                        Figure 2

Obviously the input is coupled by the capacitive transformer so the AC mathematical method would not be accurate. Here is the results anyway which might be interesting to see how both the energy and power equations suggest this device should be might make an overunity device. 

Let’s look at the oscilloscope images first to see what the results were of the test. There are three images the control test (which is exactly wired as shown in figure 1), the test where the input side had the third capacitor in parallel and the test where the output side had the third capacitor in parallel.

                                                                    Control test

 

                                                           Input with capacitor 3

 

                                                          Output with capacitor 3

            When I first did the test I noticed that there were two options for resonance. I could either take the value where the input voltage was lowest or where the output voltage was highest. So I chose to take the value where the output was highest. There was a problem with the test with input with capacitor 3 because the frequency generator was maxed out in highest frequency possible yet it wasn’t clear that this was the maximum of the resonance. This is probably why the numbers are not great.

The c-stack had value of 50pF on the input and 100pF on the output. Capacitor 3 had a value of 100 micro-farads. The resistor had a value of 470 Ohms.  For all three tests I recorded the frequency, the input voltage and the output voltage. Here are the values:

Control : frequency: 1.042 Mhz –Voltage in: 3.36 Volts RMS – Voltage out: 1.59

Input with capacitor 3: f:3.226Mhz – Voltage in: 0.0084 – Voltage out: 0.0495

Output with capacitor 3: f:1.786Mhz – Voltage in: 0.256 – Voltage out: 1.36

Looking at the data from this experiment it seems my hypothesis is correct on my first point that increasing in input capacitance will increase the output voltage. It is incorrect on the second point which is an increase in the output capacitance will decrease the output voltage. This makes it seem that there isn’t much to the hypothesis and the equation is much too simple.  

            Using the standard AC analysis with capacitive reactance I calculated what the current should have been in the input. From this I then calculated the power. A similar procedure was done on the output side except I only calculated the power across the resistor because this represented a resistive load. I then took the ratio of the power output across the resistor divided by the power input.

Control: P-in/P-out: 1.523

Input with capacitor 3: 0.003212

Output with capacitor 3: 99.9

This data suggests that the output with a capacitor 3 test seems to be a good idea for further investigation as an idea for overunity implications. The data is also misleading since the device clearly does not follow conventional AC circuit mathematics.

            Using equation 1 I made another analysis of the efficiency of the tests. For this I took the energy output at the resistor divided by the energy input.

Control: W-in/W-out: 0.4487

Input with capacitor 3: 0.00003136

Output with capacitor 3: 52,410,000

This equation makes the numbers look absurd especially since 52 million times the output energy of the device seems way to incredible to be true.

For another experiment I would like to use an amplifier with the frequency generator to boost the power enough so that the amperage can be read by a meter. Another idea would be to experiment with DC charging of the c-stack and see how charges are moved into and out of the device and at what voltage.  

Bibliography:

[1] http://jnaudin.free.fr/cstack/

[2] http://www.sweethaven.com/sweethaven/ModElec/acee/lessonMain.asp?iNum=1203

[3] http://www.play-hookey.com/ac_theory/ac_rc_parallel.html