“C-stack”
Experiment
Casey Rodgers
8/21/2012
Looking
at alternative energy concepts on a website [1] I found an article written by
Cris Paltenghe. He claimed that the device disobeyed a well known energy law
that works for capacitors in an alternating circuit which is simply:
(formula
1)
Where W = energy, C = capacitance, and V = voltage.
It is a very simple
experiment to duplicate and since I had the materials I replicated it with a
frequency generator, an oscilloscope, and some copper sheet capacitors which
have silicon as the dielectric. I put two of these together with wax paper. I
haven’t bonded them together with glue or anything but when I used a capacitor
tester my dad owns the range of capacitance is around plus or minus 100pF. The
test setup is shown in the pictures below:
This is the frequency generator I used.
This is the oscilloscope I used which hooks up
to my computer.
This is the C-stack with leads taped to it.
I ran a few initial tests by tuning the device to a resonant
frequency where the output would have the highest voltage. I found that there
definitely is an anomaly with the energy stored and discharged in the capacitor
over AC cycle using the simple formula 1. With no way of testing the current in
the device I decided to try and calculate the power across the device using
conventional AC circuitry formulas (e.g. reactance, impendance, and RC series
formulas) [2,3].
After running these
tests I realized that maybe there is a correlation between the equations for
transformers and the “c-stack” which is essentially a capacitive transformer.
Using the simple equation for voltage in a capacitor and then making a ratio of
these terms. Looking at this formula I came up with the hypothesis that if the
circuit were modified with an increase in capacitance on either the input or
the output, the voltage would change. To do this a third capacitor was placed
in parallel across the c-stack on the input and then the output and none at all
for control. For each test the frequency
was adjusted to find a resonant spot that would have a peak in the secondary
voltage.
Starting with the simple equation for voltage in a
capacitor I made a ratio of these for the “primary” (or outer capacitor side)
to the “secondary” side.
This formula then makes a ratio equation:
Then re-arranged forms an equation that I used to
make two predictions for an experiment.
These predictions are: 1) If the input capacitance (C_1)
were increased, the output voltage (V_2) should increase. 2) If the output
capacitance (C_2) were increased the output voltage (V_2) should decrease.
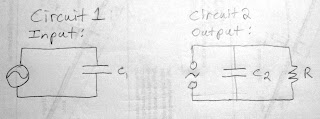
The circuit setup was
a frequency generator attached to the C-stack and the output of which had a
resistor (see figure 1). To do the AC circuit analysis I treated the input as
one circuit and the output as another (see figure 2). The third capacitor is
not shown in the figures but was placed on the input, then the output and not
at all for the control test.
Figure 1
Figure 2
Obviously the input is
coupled by the capacitive transformer so the AC mathematical method would not
be accurate. Here is the results anyway which might be interesting to see how
both the energy and power equations suggest this device should be might make an
overunity device.
Let’s look at the
oscilloscope images first to see what the results were of the test. There are
three images the control test (which is exactly wired as shown in figure 1),
the test where the input side had the third capacitor in parallel and the test
where the output side had the third capacitor in parallel.
Control test
Input with capacitor 3
Output with capacitor 3
When
I first did the test I noticed that there were two options for resonance. I
could either take the value where the input voltage was lowest or where the
output voltage was highest. So I chose to take the value where the output was
highest. There was a problem with the test with input with capacitor 3 because
the frequency generator was maxed out in highest frequency possible yet it wasn’t
clear that this was the maximum of the resonance. This is probably why the
numbers are not great.
The c-stack had value
of 50pF on the input and 100pF on the output. Capacitor 3 had a value of 100
micro-farads. The resistor had a value of 470 Ohms. For all three tests I recorded the frequency,
the input voltage and the output voltage. Here are the values:
Control : frequency: 1.042 Mhz –Voltage in: 3.36 Volts
RMS – Voltage out: 1.59
Input with capacitor 3: f:3.226Mhz – Voltage in: 0.0084
– Voltage out: 0.0495
Output with capacitor 3: f:1.786Mhz – Voltage in:
0.256 – Voltage out: 1.36
Looking at the data from this experiment it seems my
hypothesis is correct on my first point that increasing in input capacitance
will increase the output voltage. It is incorrect on the second point which is
an increase in the output capacitance will decrease the output voltage. This makes
it seem that there isn’t much to the hypothesis and the equation is much too
simple.
Using
the standard AC analysis with capacitive reactance I calculated what the
current should have been in the input. From this I then calculated the power. A
similar procedure was done on the output side except I only calculated the
power across the resistor because this represented a resistive load. I then
took the ratio of the power output across the resistor divided by the power input.
Control: P-in/P-out: 1.523
Input with capacitor 3: 0.003212
Output with capacitor 3: 99.9
This data suggests that the output with a capacitor
3 test seems to be a good idea for further investigation as an idea for
overunity implications. The data is also misleading since the device clearly
does not follow conventional AC circuit mathematics.
Using
equation 1 I made another analysis of the efficiency of the tests. For this I
took the energy output at the resistor divided by the energy input.
Control: W-in/W-out: 0.4487
Input with capacitor 3: 0.00003136
Output with capacitor 3: 52,410,000
This equation makes the numbers look absurd
especially since 52 million times the output energy of the device seems way to
incredible to be true.
For another experiment
I would like to use an amplifier with the frequency generator to boost the
power enough so that the amperage can be read by a meter. Another idea would be
to experiment with DC charging of the c-stack and see how charges are moved
into and out of the device and at what voltage.
Bibliography:
[1] http://jnaudin.free.fr/cstack/
[2] http://www.sweethaven.com/sweethaven/ModElec/acee/lessonMain.asp?iNum=1203
[3] http://www.play-hookey.com/ac_theory/ac_rc_parallel.html